EECS 31/CSE 31/ICS 151 Homework 6 Questions with Solutions

View Questions Only
View Questions with Strategies

Problem 1

Question

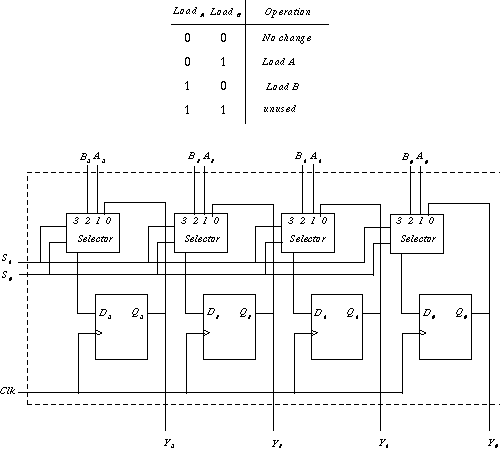
(Registers) Design a register with two load signals, that enable the loading of data from two different sources.

Solution

Problem 1 Answer

Problem 2

Question

(Shift-Registers) Using a 4-bit shift register, construct a 4-bit register that can rotate its content one position to the left or right.

Solution

Problem 2 Answer Logic Schematic

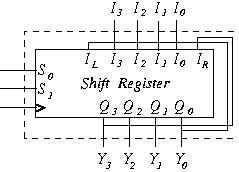
Logic Schematic

Problem 3

Question

(Counters) Design a 4-bit binary counter that counts up only in:

  1. Even numbers (0, 2, 4, 6, 8, ...)

Solution

  1. Develop state/output table.
    PRESENT STATE NEXT STATE
    Q3 Q2 Q1 Q0 Q3(next) Q2(next) Q1(next) Q0(next)
    0 0 0 0 0 0 1 0
    0 0 1 0 0 1 0 0
    0 1 0 0 0 1 1 0
    0 1 1 0 1 0 0 0
    1 0 0 0 1 0 1 0
    1 0 1 0 1 1 0 0
    1 1 0 0 1 1 1 0
    1 1 1 0 0 0 0 0
  2. Write the next-state equations. 
     Q3(next) = Q3Q1' + Q3Q2' + Q3'Q2Q1
 Q2(next) = Q2Q1' + Q2'Q1
 Q1(next) = Q1'
 Q0(next) = 0
  3. Draw logic schematic.

    Problem 3 Answer Logic Schematic

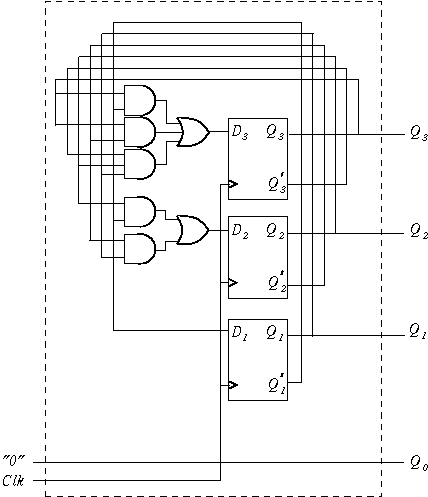
Problem 4

Question

(Register files) Design an 8 x 4 register file with:

  1. One write and two read ports

Solution

Problem 4 Answer

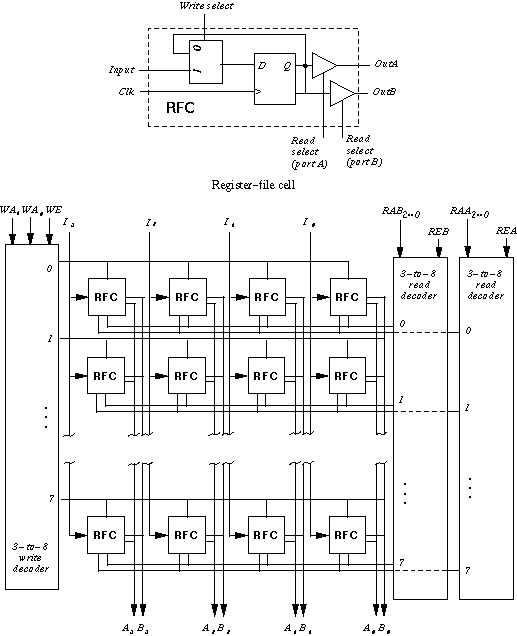
Problem 5

Question

(Memories) Design:

  1. 256K x 8 RAM using 256K x 1 RAM chips

Solution

Problem 5 Answer

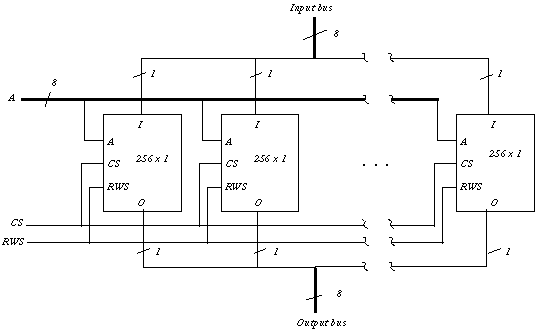
Problem 6

Question

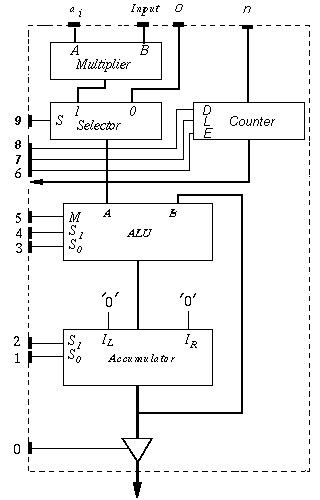
(Datapaths) Design a simple datapath that can compute the expression:

  1. Sum Imageaixi

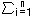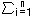  2. Sum Imageaixi + bi

Solution

  1. Problem 6 Answer: Sum aixi
  2. Problem 6 Answer: Sum aixi+bi

Problem 7

Question

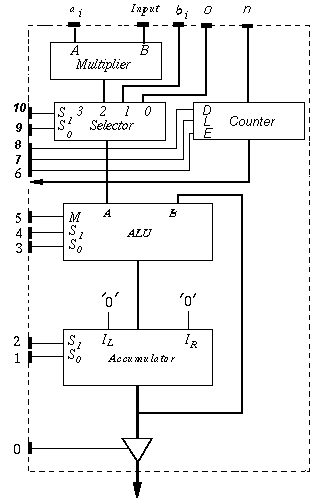
(Datapaths) Define and implement the controller for the datapath that couldexecute the algorithm developed in Problem 7.19(a).

Solution

  1. Write out the basic algorithm. 
    
sum := 0
loop:
    for i = 1 to n
    sum := sum + aixi 
end loop
output := sum
  2. Assign the vaiable to the registers. Here ai and xi and are inputs, don't need extra registers to store them, we use couter to store n, accumulator to store sum.
  3. Derive the proper control word for each statement.
    Selector
    (S)    		 Counter
    (D L E)    		 ALU
    (M S1 S0)    		 Accumulator
    (S1 S0)    		 Output
    (OE)
    0 x 1 x 0 0 1 0 1 0
    1 1 0 1 1 0 1 0 1 0
    x x x x 0 0 0 0 0 1

  4. Develop state diagram (FSM representation) for the above algorithm.

    Problem 7 state diagram

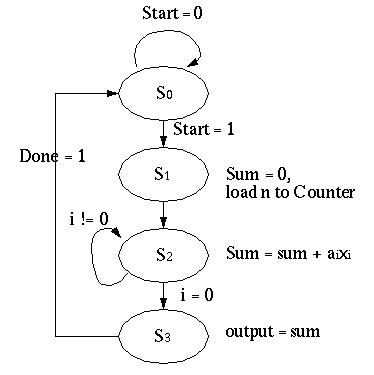
  5. Draw next-state table, write next-state equations.
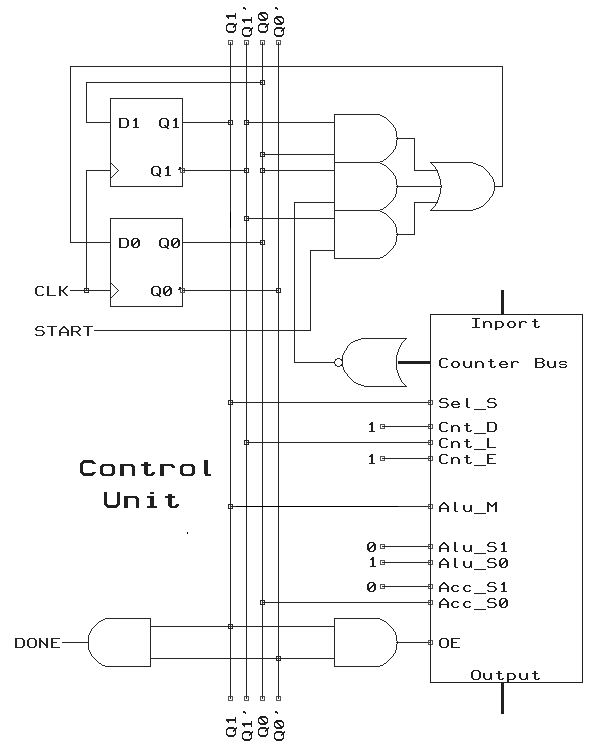
    STATES Q1Q0 Start, (i = 0)
    00 01 11 10
    S0 00 00 00 01 01
    S1 01 11 11 11 11
    S2 11 11 10 10 11
    S3 10 00 00 00 00 
     Q1(next)Q0(next)
 Q1(next) = Q0
 Q0(next) = Q1'Q0 + Q0(i = 0)' + Q1'Start
  6. Draw output logic table, write output equations.
    STATE Q1Q0 Selector
    (S)    		 Counter
    (D L E)    		 ALU
    (M S1 S0)    		 Accumulator
    (S1 S0)    		 Output
    (OE)
    S0 00 x x x x x x x x x x 0
    S1 01 0 1 0 1 1 0 1 0 1 0
    S2 11 1 1 0 1 1 0 1 0 1 0
    S3 10 x x x x x x x 0 0 1 
     Sel_S = Q1
 Cnt_D = 1
 Cnt_L = Q1'
 Cnt_E = 1
 Alu_M = Q1
 Alu_S1 = 0
 Alu_S0 = 1
 Acc_S1 = 0
 Acc_S0 = Q0
 OE = Q1Q0'
  7. Develop logic schematic.

    Problem 7 logic schematic